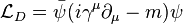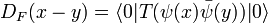In quantum field theory, a fermionic field is a quantum field whose quanta are fermions; that is, they obey Fermi-Dirac statistics. Fermionic fields obey canonical anticommutation relations rather than the canonical commutation relations of bosonic fields. The prominent example is the Dirac field which can describe spin-1/2 particles: electrons, protons, quarks, etc. The Dirac field is a 4-component spinor. It can also be described by two 2-component Weyl spinors. Spin-1/2 particles that have no antiparticles (possibly the neutrinos) can be described by a single 2-component Weyl spinor (or by a 4-component Majorana spinor, whose components are not independent).
Contents
- 1 Basic properties
- 2 Dirac fields
- 3 See also
- 4 References
1.Basic properties
Free (non-interacting) fermionic fields obey canonical anticommutation relations, i.e., involve the anticommutators {a,b} = ab + ba rather than the commutators [a,b] = ab − ba of bosonic or standard quantum mechanics. Those relations also hold for interacting fermionic fields in the interaction picture, where the fields evolve in time as if free and the effects of the interaction are encoded in the evolution of the states.
It is these anticommutation relations that imply Fermi-Dirac statistics for the field quanta. They also result in the Pauli exclusion principle: two fermionic particles cannot occupy the same state at the same time.
2.Dirac fields
The prominent example of a spin-1/2 fermion field is the Dirac field (named after Paul Dirac), and denoted by ψ(x). The equation of motion for a free field is the Dirac equation, 
where  are gamma matrices and m is the mass. The simplest possible solutions to this equation are plane wave solutions,
are gamma matrices and m is the mass. The simplest possible solutions to this equation are plane wave solutions,  and
and 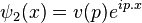 . These plane waveψ(x), allowing for the general expansion of the Dirac field as follows, solutions form a basis for the Fourier components of
. These plane waveψ(x), allowing for the general expansion of the Dirac field as follows, solutions form a basis for the Fourier components of
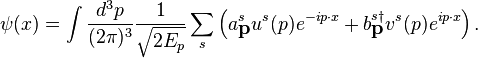
The  and
and 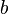 labels are spinor indices and the
labels are spinor indices and the  indices represent spin labels and so for the electron, a spin 1/2 particle, s = +1/2 or s=-1/2. The energy factor is the result of having a Lorentz invariant integration measure. Since
indices represent spin labels and so for the electron, a spin 1/2 particle, s = +1/2 or s=-1/2. The energy factor is the result of having a Lorentz invariant integration measure. Since  can be thought of as an operator, the coefficents of its Fourier modes must be operators too. Hence,
can be thought of as an operator, the coefficents of its Fourier modes must be operators too. Hence, 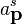 and
and 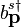 are operators. The properties of these operators can be discerned from the properties of the field.
are operators. The properties of these operators can be discerned from the properties of the field.  and
and  obey the anticommutation relations
obey the anticommutation relations

By putting in the expansions for  and
and 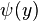 , the anticommutation relations for the coefficents can be computed.
, the anticommutation relations for the coefficents can be computed.

In a manner analogous to non-relativistic annihilation and creation operators and their commutators, these algebras lead to the physical interpretation that  creates a fermion of momentum
creates a fermion of momentum  and spin s, and
and spin s, and  creates an antifermion of momentum
creates an antifermion of momentum  and spin r. The general field
and spin r. The general field  is now seen to be a weighed (by the energy factor) summation over all possible spins and momenta for creating fermions and antifermions. Its conjugate field,
is now seen to be a weighed (by the energy factor) summation over all possible spins and momenta for creating fermions and antifermions. Its conjugate field,  , is the opposite, a weighted summation over all possible spins and momenta for annihilating fermions and antifermions.
, is the opposite, a weighted summation over all possible spins and momenta for annihilating fermions and antifermions.
With the field modes understood and the conjugate field defined, it is possible to construct Lorentz invariant quantities for fermionic fields. The simplest is the quantity  . This makes the reason for the choice of
. This makes the reason for the choice of  clear. This is because the general Lorentz transform on
clear. This is because the general Lorentz transform on 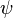 is not unitary so the quantity
is not unitary so the quantity  would not be invariant under such transforms, so the inclusion of
would not be invariant under such transforms, so the inclusion of  Lorentz invariant quantity, up to an overall conjugation, constructable from the fermionic fields is
Lorentz invariant quantity, up to an overall conjugation, constructable from the fermionic fields is  . is to correct for this. The other possible non-zero
. is to correct for this. The other possible non-zero
Since linear combinations of these quantities are also Lorentz invariant, this leads naturally to the Lagrangian density for the Dirac field by the requirement that the Euler-Lagrange equation of the system recover the Dirac equation.
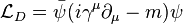
Such an expression has its indices suppressed. When reintroduced the full expression is

Given the expression for ψ(x) we can construct the Feynman propagator for the fermion field:
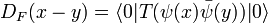
we define the time-ordered product for fermions with a minus sign due to their anticommuting nature

Plugging our plane wave expansion for the fermion field into the above equation yields:

where we have employed the Feynman slash notation. This result makes sense since the factor

is just the inverse of the operator acting on  in the Dirac equation. Note that the Feynman propagator for the Klein-Gordon field has this same property. Since all reasonable observables (such as energy, charge, particle number, etc.) are built out of an even number of fermion fields, the commutation relation vanishes between any two observables at spacetime points outside the light cone. As we know from elementary quantum mechanics two simultaneously commuting observables can be measured simultaneously. We have therefore correctly implemented Lorentz invariance for the Dirac field, and preserved causality.
in the Dirac equation. Note that the Feynman propagator for the Klein-Gordon field has this same property. Since all reasonable observables (such as energy, charge, particle number, etc.) are built out of an even number of fermion fields, the commutation relation vanishes between any two observables at spacetime points outside the light cone. As we know from elementary quantum mechanics two simultaneously commuting observables can be measured simultaneously. We have therefore correctly implemented Lorentz invariance for the Dirac field, and preserved causality.
More complicated field theories involving interactions (such as Yukawa theory, or quantum electrodynamics) can be analyzed too, by various perturbative and non-perturbative methods.




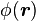
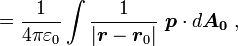





 a unit normal to the surface. The right side vanishes as the volume shrinks, inasmuch as ρb is finite, indicating a discontinuity in E, and therefore a surface charge. That is, where the modeled medium includes a step in permittivity, the polarization density corresponding to the dipole moment density p(r) = χ(r)E(r) necessarily includes the contribution of a surface charge.
a unit normal to the surface. The right side vanishes as the volume shrinks, inasmuch as ρb is finite, indicating a discontinuity in E, and therefore a surface charge. That is, where the modeled medium includes a step in permittivity, the polarization density corresponding to the dipole moment density p(r) = χ(r)E(r) necessarily includes the contribution of a surface charge.
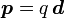









 are gamma matrices and m is the mass. The simplest possible solutions to this equation are plane wave solutions,
are gamma matrices and m is the mass. The simplest possible solutions to this equation are plane wave solutions,  and
and 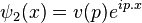 . These plane wave
. These plane wave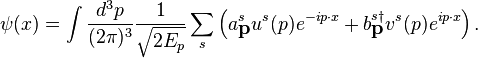
 and
and 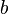 labels are spinor indices and the
labels are spinor indices and the  indices represent spin labels and so for the electron, a spin 1/2 particle, s = +1/2 or s=-1/2. The energy factor is the result of having a Lorentz invariant integration measure. Since
indices represent spin labels and so for the electron, a spin 1/2 particle, s = +1/2 or s=-1/2. The energy factor is the result of having a Lorentz invariant integration measure. Since  can be thought of as an operator, the coefficents of its Fourier modes must be operators too. Hence,
can be thought of as an operator, the coefficents of its Fourier modes must be operators too. Hence, 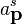 and
and 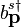 are operators. The properties of these operators can be discerned from the properties of the field.
are operators. The properties of these operators can be discerned from the properties of the field. 

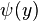 , the anticommutation relations for the coefficents can be computed.
, the anticommutation relations for the coefficents can be computed.
 creates a fermion of momentum
creates a fermion of momentum  and spin s, and
and spin s, and  creates an antifermion of momentum
creates an antifermion of momentum  and spin r. The general field
and spin r. The general field  , is the opposite, a weighted summation over all possible spins and momenta for annihilating fermions and antifermions.
, is the opposite, a weighted summation over all possible spins and momenta for annihilating fermions and antifermions. . This makes the reason for the choice of
. This makes the reason for the choice of  clear. This is because the general Lorentz transform on
clear. This is because the general Lorentz transform on 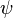 is not unitary so the quantity
is not unitary so the quantity  would not be invariant under such transforms, so the inclusion of
would not be invariant under such transforms, so the inclusion of  Lorentz invariant quantity, up to an overall conjugation, constructable from the fermionic fields is
Lorentz invariant quantity, up to an overall conjugation, constructable from the fermionic fields is  .
.