Surface charge

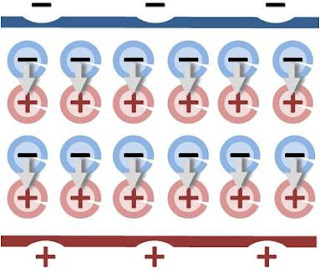
Above, discussion was deferred for the leading divergence term in the expression for the potential due to the dipoles. This term results in a surface charge. The figure at the right provides an intuitive idea of why a surface charge arises. The figure shows a uniform array of identical dipoles between two surfaces. Internally, the heads and tails of dipoles are adjacent and cancel. At the bounding surfaces, however, no cancellation occurs. Instead, on one surface the dipole heads create a positive surface charge, while at the opposite surface the dipole tails create a negative surface charge. These two opposite surface charges create a net electric field in a direction opposite to the direction of the dipoles. This idea is given mathematical form using the potential expression above. The potential is

with dA_o an element of surface area of the volume. In the event that p(r) is a constant, only the surface term survives:

 

with dA_o an elementary area of the surface bounding the charges. In words, the potential due to a constant p inside the surface is equivalent to that of a surface charge σ = p·dA, which is positive for surface elements with a component in the direction of p and negative for surface elements pointed oppositely. (Usually the direction of a surface element is taken to be that of the outward normal to the surface at the location of the element.)

If the bounding surface is a sphere, and the point of observation is at the center of this sphere, the integration over the surface of the sphere is zero: the positive and negative surface charge contributions to the potential cancel. If the point of observation is off-center, however, a net potential can result (depending upon the situation) because the positive and negative charges are at different distances from the point of observation.^[16] The field due to the surface charge is:

which, at the center of a spherical bounding surface is not zero (the fields of negative and positive charges on opposite sides of the center add because both fields point the same way) but is instead :^[17]

If we suppose the polarization of the dipoles was induced by an external field, the polarization field opposes the applied field and sometimes is called a depolarization field.^[18][19] In the case when the polarization is outside a spherical cavity, the field in the cavity due to the surrounding dipoles is in the same direction as the polarization.^[20]

In particular, if the electric susceptibility is introduced through the approximation:

then:

Whenever χ (r) is used to model a step discontinuity at the boundary between two regions, the step produces a surface charge layer. For example, integrating along a normal to the bounding surface from a point just interior to one surface to another point just exterior:

where A_n, Ω_n indicate the area and volume of an elementary region straddling the boundary between the regions, and a unit normal to the surface. The right side vanishes as the volume shrinks, inasmuch as ρ_b is finite, indicating a discontinuity in E, and therefore a surface charge. That is, where the modeled medium includes a step in permittivity, the polarization density corresponding to the dipole moment density p(r) = χ(r)E(r) necessarily includes the contribution of a surface charge.^[21][22][23]

It may be noted that a physically more realistic modeling of p(r) would cause the dipole moment density to taper off continuously to zero at the boundary of the confining region, rather than making a sudden step to zero density. Then the surface charge becomes zero at the boundary, and the surface charge is replaced by the divergence of a continuously varying dipole-moment density.